Equilibrium Solution of a Differential Equation

By Bio_Macie209 13 May, 2022 Post a Comment

If there is no value of C in the solution formula 2 which yields the solution y y0 then the solution y y0 is called a singular solution of the differential equation 1. Can a Manometer Measure Vacuum Pressure.

Equilibrium Points For Nonlinear Differential Equations Youtube

Well do a few more interval of validity problems here as well.

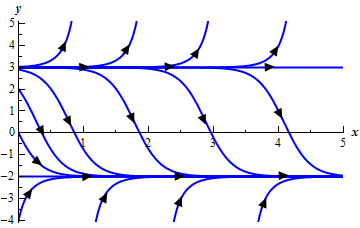
. We call the value y0 a critical point of the differential equation and y y0 as a constant function of x is called an equilibrium solution of the differential equation. A differential equation is termed as linear if it exclusively involves linear terms that is terms to the power 1 of y y y or higher order and all the coefficients depend on only one variable x as shown in Eq. In mathematics specifically in differential equations an equilibrium point is a constant solution to a differential equation.

87-S1-Q5 Integration by substitution. When measuring vacuum with an open manometer the. Bernoulli Differential Equations In this section well see how to solve the Bernoulli Differential Equation.

Calculate the pressure using the open manometer equation. The density of mercury ρ is 13500 kgm3. Vacuum is a pressure that is less than atmospheric pressure.

Section 9-1. Formal definition edit The point x R n displaystyle tilde mathbf x in mathbb R n is an equilibrium point for the differential equation. Exact Equations Identifying and solving exact differential equations.

Well leave the detail to you to get the general solution. This differential equation is separable and linear either can be used and is a simple differential equation to solve. This section will also introduce the idea of using a substitution to help us solve differential.

The pressure differential across the orifice can be used to calculate the flow rate using the orifice equation. Okay back to the differential equation that ignores all the outside factors. Before we get into actually solving partial differential equations and before we even start discussing the method of separation of variables we want to spend a little bit of time talking about the two main partial differential equations that well be solving later on in the chapter.

The differential equation can also be classified as linear or nonlinear. However a lot of textbook other materials about differential equation would start with these example mainly because these would give you the most fundamental form of differential equations based on Newtons second law and a lot of real life examples are derived from these examples just by adding some realistic factors eg damping frictions external forces etc. Solution to a differential equation.

The Stability Of Equilibria Of A Differential Equation Youtube